The coefficient of friction, with the symbol µ is the constant in the friction equation, F = µR.

It is the ratio of the force of friction acting between two surfaces in contact, and the force needed to slid one over the other.

Coefficient of friction, friction coefficient or frictional coefficient, as it is also known, cannot be determined by calculations, but by experiment. Its values depend on the materials in contact with each other, and it ranges from near zero to above one.

If coefficient of friction is zero, it means there is no friction existing between the surfaces. However, this is only a hypothetical value, since no surfaces in contact has been found to be frictionless.

The higher the value of coefficient of friction, the greater the frictional force acting between the surfaces, and this means a higher force will be needed to slid one of them over the other.

In comparison, the coefficient of static friction for two particular surfaces is usually found to be higher than their coefficient of kinetic friction. This goes with the fact that static friction is higher than kinetic friction, however, there are certain surfaces whose coefficient of static and kinetic friction are the same. Examples of these kinds of surfaces include Teflon on Teflon surface. 

Experiment To Determine The Coefficient Of Static Friction

The coefficient of static friction, µ between two surfaces in the form of a plane, see diagram below, is to place a body on the plane, and gradually increase the angle of inclination θ of the plane until the body is just about to slide down the plane.

The coefficient of static friction, µ can be shown to be µ = tanθ

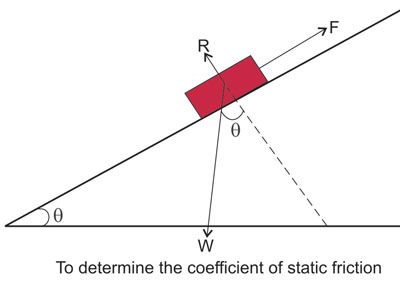
Proof: Let R be the normal reaction and F the static or limiting frictional force acting when the body is about to slide down.

Resolving along the plane for equilibrium,

F = Wsinθ   --- equation (1)

Resolving perpendicular to the plane,

R = Wcosθ   ---equation (2) 

Dividing equation (1) by (2),

^F/_R = µ = ^Wsinθ/_Wcosθ

                                                    = tanθ

The coefficient of friction, µ, for some surfaces are given below:

Wood on wood   --- 0.3 – 0.5

Wood on metal ---  0.6

Metal on metal --- 0.15 – 0.2

Metal on greased metal ---  0.1

Wood on stone  ---  0.6 – 0.7

Read about friction here
Read about static friction here
Read about kinetic friction here
Read calculating friction here