The coefficient of kinetic friction between two surfaces can be determined in the laboratory using the same experiment as that of kinetic friction:

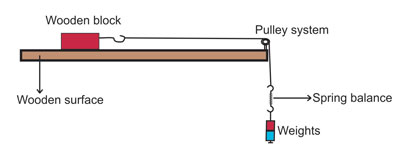
By the addition of the right weights that makes the block to move at constant velocity, the net force acting on the body becomes zero.

Then, considering all forces acting on the block, horizontally and vertically as shown below:

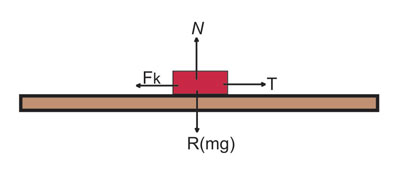
Resolving horizontal forces:

Kinetic frictional force, F_k minus the Tension on the string equals zero. That is,

F_k – T = 0

F_k - T = 0

F_k = T

  From the formula of kinetic friction, F_k  = µ_k N

Since F_k = T, then

T = µ_k N

Since the Tension on the string equals the attached weights, Mg, then,

  Mg =  µ_k N   --- equation 1

Resolving vertical forces:

Normal force N acting on the block minus weight of the block mg equals zero. That is,

N – mg = 0

N = mg

Substituting mg for N in equation 1, we have,

Mg = µ_k mg

Therefore  µ_k = ^Mg/_mg

See kinetic friction here
See static friction here
See coefficient of static friction here
See friction here
See calculating friction here