|
Calculating
the values of friction forces acting between the surfaces of two bodies in
contact with each other, using friction formula and equation, and applying the
concept of static friction.
Question 1:
A body of mass 5kg is placed on a horizontal plane. It is
found that a force of 10N applied horizontally to the body is just about to move
it. Calculate the coefficient
of static friction between the body and the plane.
Solution
Given: since the force of 10N was applied when the body was
just about to move, then the static or limiting frictional force, F = 10N
The normal reaction R on the body is equal to its weight.
i.e., weight = mass x acceleration due to gravity (10m/s2)
R = W
=
5 x 10
=
50 Newtons
Therefore, from the formula of friction,
F = µ
R
µ = F/R
= 10/50
= 0.2
The coefficient of static friction between the body and the
plane is 0.2
Question 2:
A body of mass 40kg is given an acceleration of
10m/s2 on
horizontal ground for which the coefficient
of friction is 0.5. Calculate the force required to accelerate the body.
(Take g = 10m/s2)
Solution
Notice that the body is accelerated, which means the force
that acted on it is more than the limiting frictional force.
Therefore, the equation of motion of the body is given as:
F - µR
= ma
F represents the applied force
µR
represents the force of friction
ma represents the net or resultant force
F = ma + µR
= 40 x
10 + (0.5 x 40 x 10)
= 400 +
200
= 600N
The force required to accelerate the body is 600 Newtons.
Question 3:
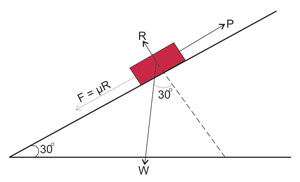
A body of weight W is placed on a rough inclined plane with
angle of inclination30o. Calculate the coefficient of static friction
if the body is just on the point of slipping.
Solution

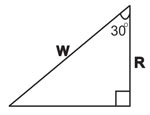
The diagram above shows a body on an inclined plane and the
different forces acting on it.
R represents the normal reaction
F represents the static
or limiting frictional force
W represents the weight
of the body.
Now, we have to resolve the forces along the plane for
equilibrium, and perpendicular to the plane.
Resolving along the plane for equilibrium:
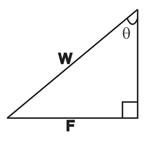
F = Wsinθ
--- equation (1)
Resolving perpendicular to the plane:
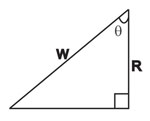
R = Wcosθ
--- equation (2)
Since at the point of sliding, frictional force is
proportional to the normal reaction, giving the equation
F = µR
Therefore, µ =
F/R
Now dividing equation (1) above by equation (2), we have
F/R =
Wsinθ/Wcosθ
= µ
µ
= Wsinθ/Wcosθ
µ
= tanθ
Therefore, the coefficient of
friction, µ
for a body on an inclined plane is always given as the tangent of the angle of
inclination.
Answering the question: the coefficient of friction of the
body on an inclined plane with angle of inclination 30o is
Tan30o = 1/√3
= 0.58
Question
4:
A body of mass 4kg is on the point of slipping down a
plane, which is inclined at 30o to the horizontal. What force, parallel to the
plane, will just move it up the plane? (Take g = 10m/s2).
Solution
Let P be the force needed to move the body up the plane,
and F = µR
the limiting frictional force opposing the motion. Notice that the difference of
the forces on the body along the plane is P - µR
since P will be greater than the frictional force µR,
for the body to be moved up.
Resolving along the plane for equilibrium:
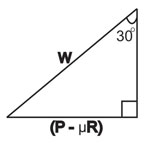
Sin30o =
(P – µR)/W
P – µR
= Wsin30o
P = µR
+ Wsin30o --- equation (1)
Resolving perpendicularly to plane:
Cos30o = R/W
R = Wcos30o --- equation (2)
Substituting Wcos30o for R in equation (1), we
have
P = µWcos30o
+ Wsin30o
Remember that
µ
= tanθ
Therefore,
µ =
tan30o = 1/√3
P = 1/√3
x W x √3/2
+ W x 1/2
P = W/2 + W/2
P = W
W = weight of the body = m x g
=
4 x 10
= 40N
Therefore, the force that is needed to just move the body
up the plane is 40 Newtons.
Read
about friction here
Read about static friction here
Read
about kinetic friction here
|