|
From
Newton's second law of motion, we have established that the force that acts on a
body can be calculated by using the formula:
F = ma
Where
F stands for force;
m for the mass of the body, and a
the acceleration of the body.
From the
formula for force above, to calculate the force that acts on a body, we simply
multiply its mass, which is measured in kilogram (kg) with its acceleration
measured in metre per second squared (ms-2).
The
acceleration of a body is the rate of change in its velocity. Stating it in
mathematical term:
Acceleration (a) = ∆v/t.
The
symbol ∆
is called delta, and it represents a
change in the value of a property. ∆v
therefore stands for a
change in velocity.
∆v = displacement / time
Therefore,
acceleration = displacement/t2 and this is why the SI unit of
acceleration is metres per second squared.
Hence,
another way of stating the formula for force is:
Force = mass x displacement/time2
The SI unit
of force is the Newton (N). This means that after you have calculated the
quantity of force on a body, you must express it in Newtons.
Remember
that in physics calculations, all quantities are expressed in their respective
units.
Question
1.
Calculate
the magnitude of an external force which acts on a particle of mass 0.15kg for
0.03s and changes its speed by 20m/s.
Solution:
Given:
Mass
of particle = 0.15kg, change of velocity (∆v)
= 20ms-1, time of change of velocity = 0.03s
Using the
formula for force,
F = m x ∆V/t
F =
0.15 x 20/0.03
F = 5
x 20 = 100N
The
magnitude of the force which acted on the particle is 100 Newtons.
Question
2.
A ball of
mass 0.1kg approaching a tennis player with a velocity of 10ms-1, is hit back in
the direction opposite with a velocity of 15ms-1. If the time of impact between
the racket and the ball is 0.01s, calculate the magnitude of the force with
which the ball is hit.
Solution:
Given:
Change
in velocity (∆v
= v - u), where v is the final velocity, i.e. the velocity the
ball was hit back, and u is the initial velocity, i.e. the velocity with which
the ball was approaching the player.
Therefore,
change
in velocity, ∆v
= 15ms-1 - 10ms-1 = 5ms-1
Mass =
0.1kg, time of change of velocity = 0.01s.
Using the
formula for force,
F = m
x ∆V/t
F =
0.1 x 5/0.01
F =
50N
The
magnitude of the force with which the ball is hit is 50 Newtons.
Question
3.
A body of
mass 20kg is set in motion by two forces 3N and 4N, acting at right angles to
each other. Determine the magnitude of its acceleration.
Solution:
Since we
have two forces acting on the body at right angles to each other, we first have
to resolve them to determine the magnitude of the force that actually moves the
body. This we can do using a right angled triangle.
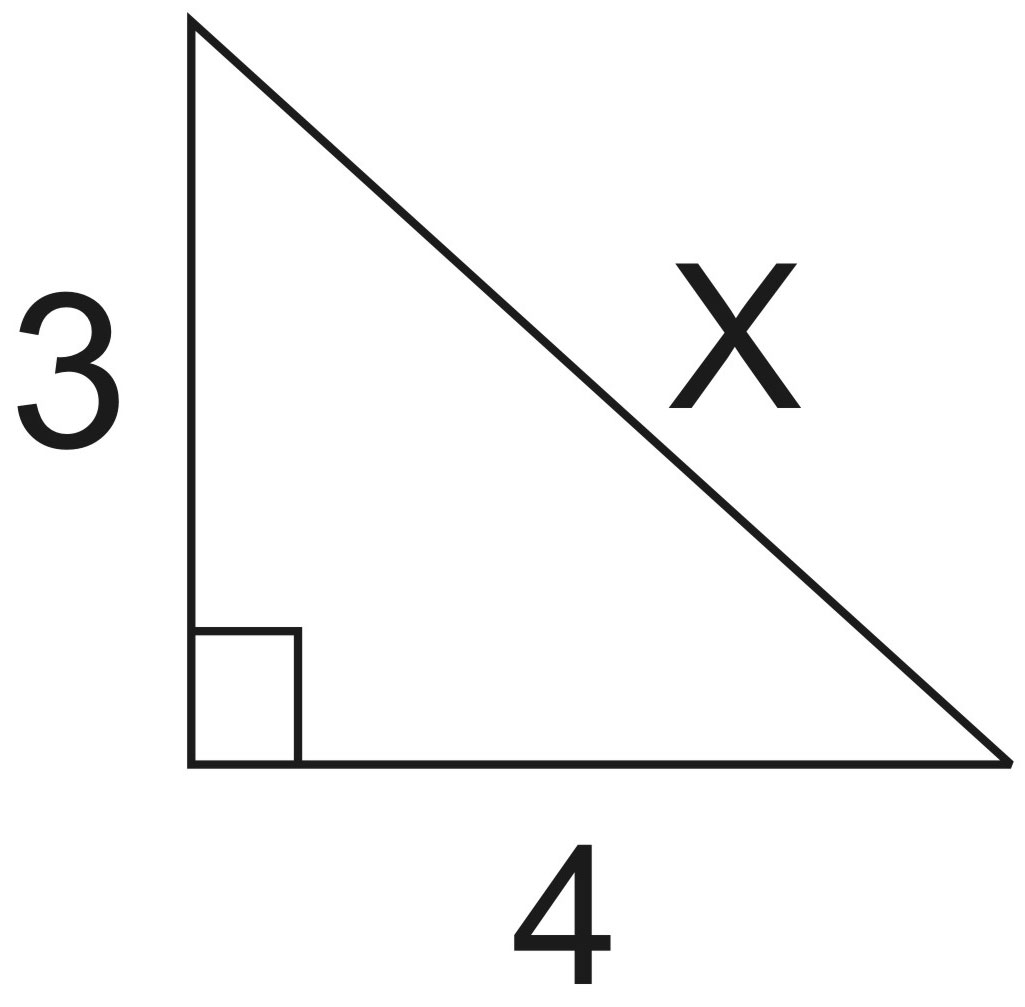
x represents
the net force, which actually moves the body.
Using
Pythagora's theorem, we have
x2
= 32 + 42
x2
= 9 + 16
x2
= 25
x = 5
Therefore,
net force equals 5 Newtons.
Now to
calculate the magnitude of its acceleration:
Using the
formula for force,
F = ma
where force
is 5N and mass 20kg
therefore,
5 = 20
x a
a =
5/20 = 0.25
The
magnitude of the body's acceleration is 0.25 m/s2
Question
4.
A net force
of magnitude 0.6N acts on a body of mass 40g, initially at rest. Calculate the
magnitude of the resulting acceleration.
Solution:
Given:
Magnitude of
force that acts on the body = 0.6 Newtons, mass of body = 40g. The SI unit of
mass is kilogram, therefore converting mass in gram to kilogram by dividing 40g
by 1000 gives the mass of body in kilogram = 0.04kg.
Using the
formula for force,
F = ma
0.6 =
0.04 x a
a =
0.6/0.04 = 15
The
resulting acceleration is 15m/s2
Question
5.
A bullet of
mass 120g is fired horizontally into a fixed wooden block with a speed of 20ms-1. The bullet is brought to rest in the block in 0.1s by a constant
resistance. Calculate the: (i) magnitude of the resistance (ii) distance, moved
by the bullet in the wood.
Solution:
Note: the
resistance is the force which acted on the bullet and brought it to rest (or to
a complete stop). A resistance is a force, however, it does not cause an object
to move, but to slow it down or to stop it completely.
When an
object is brought to rest, it means it has been stopped completely - no more
movement. And that means that its final velocity is zero.
Mass of
bullet 0.12kg (converting 120g to kilogram, initial velocity = 20ms-1,
final velocity = 0, time of change of velocity = 0.1s.
∆v =
final velocity (zero) - initial velocity
final
velocity = 0 because the bullet was brought to rest.
Therefore, ∆v
= 20ms-1
(i)
Using the formula for force, F = m x
∆V/t
F = 0.12 x
20/0.1 = 24N
The
resistance is 24N
(ii) To find
the distance moved by the bullet in the wood, we can use one of the equations of
motion,
S = (v+u)/2
x t
Where S =
distance moved by the bullet, v = final velocity, u = initial velocity,
t =
time.
S = (0
+ 20) / 2 x 0.1
S = 1m
Therefore,
distance moved by the bullet in the wood = 1m
See more calculations based on Newton's second law of motion.
|